O que é um Box Plot? Botplot Bloxpot
O gráfico box plot, frequentemente escrito como botplot ou bloxara determinar a média e os os quartis corretamente, sempre organize os valores <b>em ordempot, é uma ferramenta estatística essencial na estatística descritiva para interpretar a distribuição de dados quantitativos. Ele permite a interpretação da dispersão dos dados e comparação de grupos de forma eficiente.
Ao longo deste artigo, explicaremos como interpretar um gráfico box plot, quais são seus principais componentes e como construí-lo facilmente (clique aqui para construi-lo online).
💡 Curiosidade: As escrita “boxplot”, “botplot” e “bloxpot” ocorre devido à similaridade fonética, mas o termo correto é box plot ou boxplot.
Para interpretação do gráfico boxplot precisamos primeiramente compreender seus componentes e a posição de cada um.
Mediana
A mediana (quartil 2) é o valor central de um conjunto de dados ordenado. Ela divide o conjunto em duas partes iguais, com 50% dos dados abaixo e 50% acima dela.
Exemplo prático
Considere os dois grupos de dados abaixo de Índice de Massa Corporal (IMC) organizados em ordem crescente:
Se o seu professor ou professora te perguntar “Qual numero está na posição central no conjunto de dados?” você pode facilmente responder, no grupo A o numero que ocupa a posição central é o 24 e no grupo B o ponto central está entre os números 23 e 24.
Perfeito! Exatamente isso. No grupo A temos 11 valores (ímpar) ou seja, antes do 24 temos cinco valores e depois mais cinco valores. Sempre que o conjunto de dados for ímpar haverá um número que se encaixa perfeitamente ao centro do conjunto de dados que estiver em ordem crescente!Já no grupo B, temos 10 valores (par) sendo o ponto central entre os numeros 23 e 24, neste caso a média destes dois números é a mediana (Mediana: (23+24) / 2 = 23,5). Sempre que o conjunto de dados dor par o ponto central estará entre dois número e a média destes será a mediana também conhecida no box plot como quartil 2.💡 Dica: Para determinar a média e os os quartis corretamente, sempre organize os valores em ordem!
Quartil 1 e Quartil 3
Além da mediana (quartil 2), um box plot apresenta os quartis 1 e 3, que dividem os dados em 4 partes de 25% cada.
Considere o grupo B abaixo, o ponto central com a barra verde. A primeira parte de 19 a 23 corresponde a 50% dos dados e o valor 21 está bem no centro desta primeira parte sendo ele então o 1º quartil. Desta forma podemos dizer que 25% dos valores do conjunto de dados apresentam resultados menores que 21. Por isso o quartil 1 também é chamado de percentil 25.Já na segunda parte após a mediana que vai do valor 24 ao 20 temos o número 27 ocupando a posição central. Neste caso ele é o 3º quartil e podemos dizer que 75% dos valores do conjunto de dados são menores que 27. Por isso o quartil 3 também é chamado de percentil 75.Resumo dos Quartis no Grupo B:
- Q1 = 21 (percentil 25%) → 25% dos valores estão abaixo dele.
- Q2 = 23,5 (percentil 50% ou mediana) → 50% abaixo e 50% acima.
- Q3 = 27 (percentil 75%) → 75% dos valores estão abaixo dele.
💡 Curiosidade: A diferença entre Q3 e Q1 é chamada de amplitude interquartil (AIQ) e mede a dispersão central dos dados.
Desta forma fica claro que o box plot separa o conjunto de dados em 4 partes de 25% em 25%, por isso temos as denominações, quartis.
Se construirmos um box plot com base nestes dados, ele fica da seguinte forma:
Você pode criar rapidamente um box plot como esse, clicando aqui.
Perceba que aqui você tem o 23,5 que é a mediana (média de 23 e 24), o 21 que é o quartil 1, o 27 que é o quartil 3 e também os valores máximos e mínimos que são 19 e 29 respectivamente.
Box Plot em Conjuntos de Dados Reais
Nos exemplos anteriores, utilizamos apenas 10 valores, mas em pesquisas acadêmicas, estudos estatísticos e ciência de dados, os conjuntos de dados podem conter dezenas, centenas ou milhares de valores.
Para visualizar grandes volumes de dados, usamos ferramentas como: ✅ Excel ✅ Jamovi ✅ R e Python ✅ SPSS e softwares estatísticos
🔹 Clique aqui para gerar seu próprio box plot online!
Abaixo temos um exemplo de um grande conjunto de dados sendo apresentado em formato de histograma e de box plot.
💡 Box plot Interpretação:
- O histograma mostra a frequência dos valores, com colunas maiores indicando maior concentração.
- O box plot concentra 50% dos dados dentro da caixa, entre Q1 e Q3.
- Os bigodes do box plot representam valores dentro do intervalo normal.
- Os pontos acima dos bigodes são outliers, ou seja, valores extremos que fogem do padrão.
Componentes de um Box Plot
Desta forma um Box Plot possui em sua estrutura os componentes:
Definições dos componentes box plot
Outliers (Valores Extremos)
Os outliers são valores atípicos que fogem do padrão geral da distribuição dos dados. Eles ocorrem quando um ou mais valores ultrapassam os limites superiores ou inferiores, também conhecidos como bigodes do box plot.
🔍 Como identificar outliers?
- No box plot, os outliers aparecem como pontos isolados acima ou abaixo dos bigodes (explicado mais a baixo).
💡 Curiosidade: Outliers podem indicar erros nos dados ou revelar informações sobre a variabilidade da amostra.
Pontuação Mínima e Máxima
Pontuação Mínima é o menor valor e a pontuação Máxima é o maior valor do conjunto de dados. Se houver outliers, esses valores extremos aparecerão fora dos limites como pontos.Primeiro Quartil (Q1) e Terceiro Quartil (Q3)
- Quartil 1 (Q1 – Percentil 25%): 25% dos dados estão abaixo desse valor.
- Quartil 3 (Q3 – Percentil 75%): 75% dos dados estão abaixo desse valor.
💡 Dica de interpretação: Quanto maior a distância entre Q1 e Q3, maior a dispersão dos valores.
Mediana (Segundo Quartil – Q2)
A mediana (Q2) divide os dados em duas metades iguais.
Amplitude Interquartil (AIQ ou IQR)
A Amplitude Interquartil (IQR – Interquartile Range) mede a dispersão dos dados centrais:
AIQ=Q3−Q1
No exemplo:
- Q1 = 21, Q3 = 27,
- AIQ = 27 – 21, então AIQ = 6
Bigodes (Limites Superiores e Inferiores)
Os bigodes representam os limites que definem valores considerados dentro do padrão observado.
- Limite Inferior = Q1 – (1,5 × AIQ)
- Limite inferior é igual ao valor do 1º quartil menos (1,5 multiplicado pela amplitude interquartil)
- Limite Superior = Q3 + (1,5 × AIQ)
- Limite superior é igual ao valor do 3º quartil mais (1,5 multiplicado pela amplitude interquartil)
Cálculo dos limites superiores e inferiores (Bigodes)
Seguindo a fórmula apresentada podemos em nosso exemplo calcular:
Limite inferior: Q1 – (1,5 x AIQ) Limite inferior: 21 – (1,5 x 6) Limite inferior: 21 – 9 Limite inferior: 12
Limite superior: Q3 + (1,5 x AIQ) Limite superior: 27 + (1,5 x 6) Limite superior: 27 + 9 Limite superior: 36
📌 Observação importante:
- Se os valores mínimos e máximos estiverem dentro desses limites, eles serão usados como os extremos do box plot.
- Se houver valores acima ou abaixo desses limites, eles são marcados como outliers.
Exemplos Práticos de BoxPlot
📊 Caso 1: Todos os valores estão dentro dos limites superiores e inferiores.
Se os valores no conjunto de dados variam de 19 a 29, então:
Como 29 está abaixo do limite superior (36), ele será o máximo no box plot.
- Box plot do IMC destacando os valores mínimo (19), máximo (29), quartil 1 (21), mediana (23,5) e quartil 3 (27), facilitando a interpretação estatística.
📊 Caso 2: Valor Extremo (Outlier) Acima do Limite
Se houver um valor 38 no conjunto de dados, ele estará acima do limite superior (36) e será marcado como outlier.
Construa Seu Próprio Box Plot
Agora que você compreende os componentes do gráfico box plot, experimente criar um gráfico com seus próprios dados!
🔹 Construa seu box plot online clicando aqui!
Por que os Gráficos Box Plot São Úteis?
O gráfico box plot é uma ferramenta estatística poderosa, pois permite interpretar rapidamente a distribuição de um conjunto de dados.
A seguir, exploramos as principais razões pelas quais os gráficos box plot são úteis na análise estatística.
A Interpretação do Box Plot Mostra a Mediana de um Conjunto de Dados
No box plot, ela é representada pela linha dentro da caixa, que divide os dados em 50% inferiores e 50% superiores.
🔹 Como interpretar a mediana no box plot?
- Se os dados forem simétricos, a mediana estará no centro da caixa.
- Se os dados forem assimétricos, a mediana estará mais próxima de um dos extremos da caixa.
A Interpretação do Box Plot Mostra a Assimetria de um Conjunto de Dados
O formato do gráfico box plot indica se os dados seguem uma distribuição simétrica ou assimétrica, o que está diretamente relacionado à normalidade dos dados.
🔹 Como identificar a assimetria no box plot?
- Distribuição Simétrica ✅
- A mediana está centralizada dentro da caixa.
- Os bigodes têm comprimentos semelhantes.
- Indica uma distribuição normal ou próxima da normal.
- Assimetria Positiva (Skew à Direita) ➡
- A mediana está deslocada para a parte inferior da caixa.
- O bigode superior é mais longo.
- Isso significa que existem valores maiores mais distantes da mediana, puxando a distribuição para a direita.
- Assimetria Negativa (Skew à Esquerda) ⬅
- A mediana está deslocada para a parte superior da caixa.
- O bigode inferior é mais longo.
- Indica que os valores menores estão mais dispersos do que os maiores.
A Interpretação do Box Plot Mostra a Dispersão de um Conjunto de Dados
Em estatística, a dispersão representa a variabilidade dos dados, ou seja, o quanto os valores se afastam da mediana.
🔹 Como analisar a dispersão no box plot?
- Caixa e bigodes curtos → Baixa dispersão, indicando que os valores estão concentrados próximos à mediana.
- Caixa e bigodes longos → Alta dispersão, sugerindo uma grande variação nos valores do conjunto de dados.
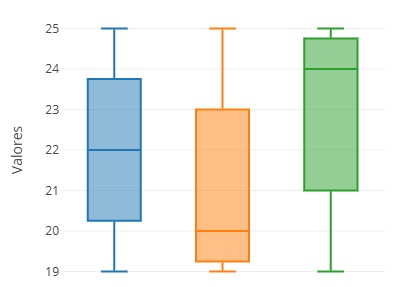
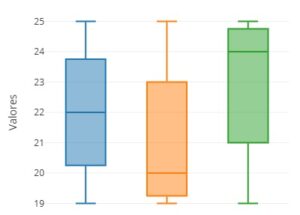
💡 Exemplo: Dois box plots com a mesma mediana, mas um com quartis mais distantes entre si, indicando maior variabilidade dos dados.
A Interpretação do Box Plot Mostra Valores Extremos (Outliers)
Os outliers são valores que se diferenciam significativamente do restante dos dados e podem indicar erros, fenômenos raros ou pontos de interesse. São representados por pontos individuais fora dos limites inferiores e superiores.
Como Comparar Gráficos Box Plot
Os gráficos box plot são extremamente úteis para comparar diferentes grupos ou amostras. Ao analisar dois ou mais box plots, é possível identificar diferenças na mediana, dispersão dos dados, outliers e assimetria.
A seguir, detalhamos um passo a passo para interpretar corretamente essas comparações.
Etapa 1: Compare as Medianas dos Box Plots
A mediana (linha dentro da caixa) é o ponto central dos dados. Quando comparando diferentes box plots, a posição da mediana pode indicar se há diferenças entre os grupos analisados.
🔹 Grafico box plot como interpretar?
- Se a mediana de um grupo está fora da caixa do outro grupo, há uma provável diferença estatística entre eles.
- Se as medianas estão dentro das caixas de ambos os grupos, os valores centrais podem ser semelhantes.
💡 Dica: É importante analisar se há significância estatística através de testes estatísticos.
Etapa 2: Compare os Intervalos Interquartis e os Bigodes
Além da mediana, o intervalo interquartil (IQR) (a altura da caixa do box plot) revela informações sobre a dispersão dos dados.
🔹 O que observar?
- Caixa maior = maior dispersão → Os dados estão mais espalhados e variam mais.
- Caixa menor = menor dispersão → Os dados estão mais concentrados.
- Bigodes longos indicam que os valores se espalham para além do intervalo interquartil.
Etapa 3: Identifique Valores Discrepantes (Outliers)
Os outliers são valores extremos que podem influenciar a interpretação dos dados. Ao comparar box plots, verifique:
- Se um grupo possui mais outliers que o outro.
- Se os outliers aparecem acima ou abaixo.
Etapa 4: Analise a Assimetria dos Dados
A assimetria (skewness) pode indicar se os dados de cada grupo apresentam padrões diferentes.
🔹 boxplot como interpretar?
- Se todos os grupos possuem o mesmo tipo de assimetria, é provável que tenham padrões semelhantes.
- Se um grupo tem uma distribuição simétrica e outro apresenta assimetria positiva ou negativa, isso pode indicar diferenças na tendência dos dados.
Próximos Passos
Gostou deste post? Caso queira aprender análises estatísticas avançadas, conheça nosso curso de estatística aplicada 👉 [Curso análise estatística clique aqui]
Se precisa de consultoria para análise de dados em sua pesquisa ou projeto, fale com nossos especialistas 👉 [Solicite uma consultoria aqui]
🔹 Construa seu próprio box plot online de forma rápida e fácil! 👉 [Clique aqui para acessar nosso gerador de box plot]
Como citar este post
Alves Junior, E. R. (2025, 25 de janeiro). Box Plot Guia Completo: Como Interpretar Gráfico Boxplot. Blog BiomedStat. Disponível em https://biomedstat.com.br/box-plot-interpretacao/